まず累乗
- \def\powercalc#1#2{
- \newcount\t \t=#1 \relax%
- \newcount\step \step=1 \relax%
- \loop%
- \multiply\t#1 \relax%
- \increment\step \relax%
- \ifnum \step<\q \repeat%
- #1=\t \relax%
- }
\loopの扱いなどについてはキヨシ関数の記事を参照。
ちなみに#○は引数。
次が階乗。
- \def\function#1{
- \newcount\t \t=1 \relax%
- \newcount\step \step=1 \relax%
- \loop%
- \multiply\t\step \relax%
- \increment\step \relax%
- \ifnum\step<#1 \repeat%
- #1=\t \relax%
- }
1から#1まで掛けるだけの簡単なお仕事。累乗とあんまり変わらない。
最後が素数判定。
- \def\ifprime#1{ %素数なら0,合成数なら1をjudgeに格納
- \ifnum #1<2 %
- %1
- \else%
- \newcount\judge \judge=0 \relax%
- \newcount\step \step=2 \relax%
- \newcount\max \max=#1 \decrement\max \relax%
- \loop%
- \newcount\temp \temp=#1 \relax%
- \surplus\temp\step \relax%
- \ifnum \temp<1 \judge=1 \fi%
- \increment\step \relax%
- \ifnum \step<\max \repeat%
- %\the\judge
- \fi%
- }
本当はtrueとかfalseとかを返せるようにしたかったのだが引数のカウンタに上書きする以外の戻り値の返し方がわかんなかったので仕方なく素数なら0,合成数なら1をjudgeに格納することにした。
Java風に言うとvoidにしてグローバル変数に格納して返す、みたいな?(適当)
3行目と14行目をコメントから外せばdviに0か1を書き出すようになる。
さて、実行。
- \documentclass{article}
- \def\surplus#1#2{%
- \newcount\n \newcount\m \newcount\t%
- \n=#1 \m=#2 \t=\n \relax%
- \divide \n by \m%
- \multiply \n by \m%
- \advance \t by -\n%
- #1=\t\relax%
- }
- \def\minus#1#2{ \advance #1 by -#2 \relax}
- \def\increment#1{ \advance #1 by 1 \relax}
- \def\decrement#1{ \advance #1 by -1 \relax}
- \def\powercalc#1#2{
- \newcount\t \t=#1 \relax%
- \newcount\step \step=1 \relax%
- \loop%
- \multiply\t#1 \relax%
- \increment\step \relax%
- \ifnum \step<\q \repeat%
- #1=\t \relax%
- }
- \def\function#1{
- \newcount\t \t=1 \relax%
- \newcount\step \step=1 \relax%
- \loop%
- \multiply\t\step \relax%
- \increment\step \relax%
- \ifnum\step<#1 \repeat%
- #1=\t \relax%
- }
- \def\ifprime#1{ %素数なら0,合成数なら1をjudgeに格納
- \ifnum #1<2 %
- %1
- \else%
- \newcount\judge \judge=0 \relax%
- \newcount\step \step=2 \relax%
- \newcount\max \max=#1 \decrement\max \relax%
- \loop%
- \newcount\temp \temp=#1 \relax%
- \surplus\temp\step \relax%
- \ifnum \temp<1 \judge=1 \fi%
- \increment\step \relax%
- \ifnum \step<\max \repeat%
- %\the\judge
- \fi%
- }
- \begin{document}
- \newcount\p \newcount\q
- \p=5 \q=3
- \powercalc\p\q
- $5^3= \the\t $
- \p=5
- \function\p
- $5!= \the\p $
- \ifprime{51}
- if $51$ is prime number? \ifnum \judge<1 Yes. \else No. \fi
- \ifprime{53}
- if $53$ is prime number? \ifnum \judge<1 Yes. \else No. \fi
- \end{document}
コメントアウトを手作業で赤くするのが疲れてきたのでやめた。
ちなみに各行の最後がコメントアウトしてあったりちょいちょい数値の後に\relaxが入ってるのはバグ防止。どっかで読んだ。
前回作った剰余演算子とインクリメント、デクリメント、減算演算子も冒頭で記述してあるが今回はインクリメントくらいしか使っていない。
累乗、階乗は戻り値がカウンタに格納されて帰ってくるので第一オペランドはカウンタでないといけない。累乗の第二オペランドと素数判定は数値でもカウンタでもいい(はず)。
55行目で5^3、60行目で5!、62,65行目で51と53が素数かどうか判定している。\ifnumで入れた数値が素数かどうか(\judgeが0かどうか)の判定でYes.かNo.か分岐。
実行結果はこう
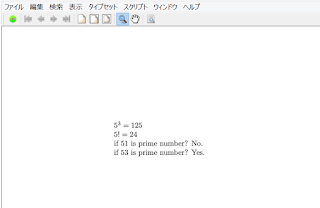
上手いこと行った。
2ケタ以上の数は{ }で括らないといけないのでカウンタのほうが楽そう。どうせ使うのはマクロの中だろうし。
配列がないので素数のリスト化とかはできず速度のこととか全く考えてないから大きい数だととてもつらい予感がする。ただベンチマークしようにも時間取得が分単位とかだから結構大変かも。
とりあえず平方根関数を使ってStep数を減らすのが当面の課題か。(でも一から実装すると平方根って2分探索とか始まったりしてやばそう。)
いつか配列を使って素数リストを書き出せるマクロでも作りたい。頑張れば連想配列のようなものができるらしいし。
-2019-03-12: \(\TeX\)を\(\mathrm\TeX\)に変更
0 件のコメント:
コメントを投稿