また前から間が空いてしまった。せっかくなので4連休で行ってきた旅行の日記をつけようと思う。
概要
2020年9月19日(土)~22日(火) の4連休、(元含む)寮の同期[1]4人で車を借り仙台発、山形・秋田・青森・岩手を周り仙台に戻ってくる旅行を行った。
メンバーは
- A氏:社会人。鉄オタ。旅慣れしているので旅行の手配をだいぶ頼っている
- B氏:M2で寮の隣人。学科柄航空オタク
- C氏:社会人。仕事柄航空オタクになった
- 筆者:酒が飲めないので自動的にハンドルキーパーになる
の4人である。
旅程詳細
9/19(Sat.)
・朝イチで東京駅に集合。東北新幹線で仙台へ。
東海道以外の新幹線は初だったのでちょっとテンションが上がった。
・仙台駅着後レンタカー屋で自動車をレンタル。
車種ははっきり確認し忘れたが日産のe-POWERとかだったと思う。モーター駆動のガス・エレクトリック式で結構運転感覚がいつもと違う。回生システムが動いているときのエンジンブレーキがものすごい。
ルームミラーがカメラの映像を映す方式だった[2]。やたらとハイテク。
余談だが仙台市内にめちゃくちゃ名鉄バスみたいな塗装のバスがいた。A氏に聞いてみると仙台交通は名鉄グループらしい。血が濃すぎでしょ。
・本格的に移動する前に仙台市内、愛子駅で一時停車。
駅メモのイベント駅であるためA氏からの要望であった。
・宮城と山形の県境あたり、天童市将棋資料館を訪問。様々な将棋駒を見学した。
・山形県銀山温泉を訪問。ちょっと手前の記念館(?)で車を停めシャトルバスで温泉街へ向かう。町並みを散策し蕎麦と豆腐を食べた。
・日も下がってきた頃、日本海沿岸、山居倉庫を訪問。
C氏の提案をそのまま旅程に入れたので知らなかったが彼から米倉としての工夫や船着場などいろいろ説明を受けた。
そのまま魚市場の海鮮を食べる計画であったがコロナの影響かネットの情報より早く閉まってしまっていた。近隣の料理店で寿司定食を食べた。
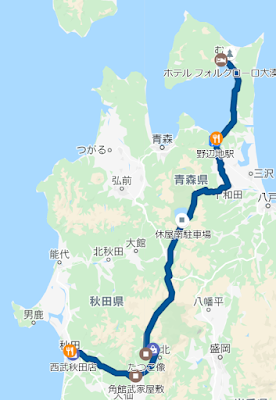
・食後、更に北上し秋田市内のホテルに宿泊。
日も暮れてきたところで借りた車がライト機能も非常に高性能であることを発見。対向車の有無などを判断し自動でハイビームを切り替えられる。信号やリフレクターなどをちゃんと判別しているようでなかなかの高精度だった。一方カメラ式のルームミラーは雨が降り出すと全く役に立たなくなった(普通のミラーと切り替えられるのでもちろん後ろは見える)。
ここまで車で270km、新幹線を含め600kmの移動。
9/20(Sun.)
・朝から移動開始。すき家で朝食を済ます。
・内陸側に西進し、角館武家屋敷を訪問。城下町の武家屋敷がたくさん保存されている。伝統工芸「樺細工」(桜の皮の利用し模様を生み出す)の展示館も見学。小豆粉から作った落雁、「もろこし」をお土産に購入。
・田沢湖へ。湖岸をほぼ一周し、たつこ像を見学、昼食に近くの食堂でラーメンを食べた。
・3時間ほど北上し青森県に突入。今度は十和田湖へ。駐車場から10分ほど歩いて十和田神社に参拝した。
夕焼けでなかなか綺麗な景色だったがスマホのカメラでは如何せん逆光で全然映らない。
・下北半島付け根あたり、野辺地駅周辺で寿司を食べた。
・ホテルに一旦チェックインした後、天体観測のため恐山へ向かう。
しかし真っ暗な山道で対向車も全然いないこともあり、C氏がビビり散らかしていたのが全員に伝染(ちなみに運転していたのは筆者である。めっちゃ怖かった。)、途中で引き返しもう少し開けたところの公園に停車した。なお天候不順のため結局星は見えずさっさと引き返してきた。
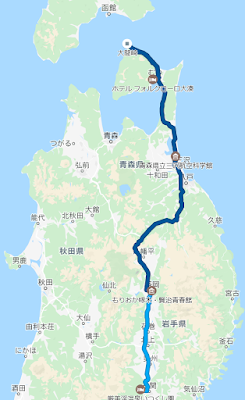
この日の移動は320km。
9/21(Mon.)
・北上し本州最北端、大間崎へ。道中太平洋沿岸から対岸、つまり北海道の陸地がほのかに見える。津軽海峡って意外と近いんですなあ。最北端では”最寄り駅”がギリギリ函館市電「湯の川」停留所になる。実質北海道。
大間で昼食にマグロ丼を食べた。めちゃくちゃ美味いわ、びっくりした。マグロそのものが美味いと感じたの初めてかもしれない(バカ舌なので)。
・来た道を戻り三沢航空科学館を訪問。当初は予定になかったが何故か航空オタクが2人もいる集団なので訪問が決定。オタクの解説を聞きながら科学館を回るとためになりますね。
十和田湖に沈められていたのが引き上げられたゼロ戦などの展示を見学。
航空科学館なのになぜか艦船の絵も展示されていた。菅野泰紀氏による写真と見紛うほどの精緻な鉛筆画で、艦内神社の慰霊ということで関係各所に奉納されているらしい。
・急に目的地を増やしたので次の目的地、花巻市の宮沢賢治記念館には閉館時間までに間に合わなくなった。観光地の夜は早い。
車中で調べたところもう少し近い盛岡市に「もりおか啄木・賢治青春館」を見つけたのでそこへ。旧銀行を改装した記念館で色々見学。
・この日は食事もつけたのでそのまま一関市の宿へ。牛を焼いて食べた。とても美味い。
青森北端から岩手南端まで2日目かけて北上した分を1日で高速で一気にかっ飛ばしたため移動距離は420kmと長め。疲れた。
9/22(Fri.)
・疲れたので宿で程々にゆっくりしつつ朝食を食べ出発。
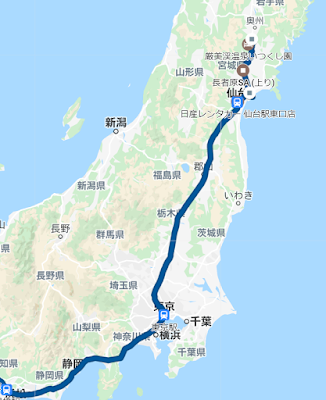
・少し北上し平泉の中尊寺へ。金色堂を始めいろいろと参拝。
・宮城県、松島へ。遊覧船に乗り島々を遊覧。その後遅めの昼食に牛タンを食べた。
・ようやくレンタカーを返却。ちょっとゆったりしすぎたか時間ギリギリになった。
車ではこの日は120km、4日間で約1100kmの移動。長い。
・仙台駅で立て替えの精算をし、駅前のカラオケで1時間歌って解散した。コロナ以来の人とのカラオケ。4日も同じ車に乗ってたんだからまあ濃厚接触も今更ですね。
・筆者はそのまま新幹線で帰省。東北→東海道とこんなに新幹線に乗ったのも初めて。
一気に620kmを駆け抜け4日間での累計移動距離は約2000kmとなった。
結び
筆者は普段食事にはあまり頓着しないのだが、今回はいろいろと美味いものを食べた。たまにはこういうのもいいなと感じられる旅行となった。
[1]: 筆者は現在県人寮に在籍中である。基本的に学部4年間専用だが若干名は2年間延長可能なのでちょいちょい院生がいる。
[2]: インテリジェントミラーというらしい。